Overview for Annuity Due Table
Annuity due table depicts the worth of the specified annuity mentioned by that table. However, the annuity due table is different for present and future value considering the time value and value of the investment.
Therefore the table helps the annuitant to take decisions while planning to invest. Moreover, we need to get a brief of annuity and its kind first leading to annuity due table.
What is an Annuity?
An annuity can be described as a kind of multi-period investment where a principal amount is deposited and then regular payments are made during the phase of investment. The payments are of fixed size.
For example, a car loan can be an annuity where the company gives the person a loan to purchase a car. However, the individual makes an initial down payment and then each month a fixed amount. The sum of the payments made altogether will be greater than the loan amount, which explains an interest rate implicity charged on the loan. As a result, the payment schedules spread over time.
The advantages of making a loan an annuity can be:
- There is a regular known cash flow
- Predictable payments and returning the amount in smaller multiple periods is advantageous for an individual overpaying the whole lot at once.
- The institution can monitor the financial health of the customers or clients
Types of Annuity
Since annuities spread over multiple periods, there are different types of annuities based on when the payments are made in the period. Following are the three types:
- Annuity due: Here the payments are made by the client at the start or beginning of the period. Like if the period is each month, the payments are made at the starting of each month.
- Ordinary Annuity: In this method, the payments are made at the end of each period. Like if the period is one month, this explains that payment is done on the 28th, 30th or 31st of each month depending on the type of month. This must be noted that mortgage payment is mostly ordinary annuities.
- Perpetuities: This explains that the payments continue forever. However, this condition is rarer than the first two types.
Annuity Due
This method describes the kind of annuity whose payment gets due at the beginning of the period immediately. One common example of an annuity due table can be rent since landlords often demand the payment at the start of a new month. Instead of collecting it after the guest has enjoyed the benefits of the apartment.

However, the future and the present value formulas differ slightly from ordinary annuity because of the differences in when the payments are made.
Calculating Annuity Due
The annuity due table payments represent an asset received legally by an individual. However, the person paying the due has the debt liability needing periodic payments.
Since the annuity due calculator payments present future cash outflows or inflows, the payer of the funds can calculate the entire amount of the annuity while factoring in the time value of money. This can be accomplished by considering the future and the present value.
Insurance companies sold annuity due calculator as a financial product that needs annuity payments to be made at the start of each month, quarter or annual period. This kind of annuity provides the companies during the distribution period with payments as long as the annuitant lives. However, as the individual passes, the insurance company retains the funds remaining.
Note: The income from annuity gets taxed as ordinary income.
Examples of Annuity due
The recurring obligation may lead to an annuity due calculator.
- Therefore, the monthly bills like car payments, mortgages, cell phone payments and rent, are few examples since the beneficiary needs to pay at the start of the billing period.
- As discussed above, insurance expenses as also annuities due as the insurer gets paid at the start of the coverage period.
- Also, annuity due table situations may arise when the annuitant saves for retirement or put their money aside for a specific reason.
Annuity Due Table
Present value of annuity due table
The present value of annuity due table is used as a quick reference to find the present value annuities. Also, It provides the figures for interest rates and discrete-time periods that may not correspond every time to the real world. Therefore, there are different formulas available for each kind. So, Few interest rates are shared below:
| n | 1% | 2% | 3% | 4% | 5% | 6% | 8% |
| 1 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 2 | 1.9901 | 1.9804 | 1.9709 | 1.9615 | 1.9524 | 1.9434 | 1.9259 |
| 3 | 2.9704 | 2.9416 | 2.9135 | 2.8861 | 2.8594 | 2.8334 | 2.7833 |
| 4 | 3.9410 | 3.8839 | 3.8286 | 3.7751 | 3.7232 | 3.6730 | 3.5771 |
| 5 | 4.9020 | 4.8077 | 4.7171 | 4.6299 | 4.5460 | 4.4651 | 4.3121 |
Future Value of Annuity due Table
This kind of annuity due table represents a factor specific to the future value of payments, given a specified interest rate. Then, the factor multiples by one of the payments or cash flow for each period to obtain a future value of the stream.
| n | 1% | 2% | 3% | 4% | 5% | 6% | 8% |
| 1 | 1.0100 | 1.0200 | 1.0300 | 1.0400 | 1.0500 | 1.0600 | 1.0800 |
| 2 | 2.0301 | 2.0604 | 2.0909 | 2.1216 | 2.1525 | 2.1836 | 2.2464 |
| 3 | 3.0604 | 3.1216 | 3.1836 | 3.2465 | 3.3101 | 3.3746 | 3.5061 |
| 4 | 4.1010 | 4.2040 | 4.3091 | 4.4163 | 4.5256 | 4.6371 | 4.8666 |
| 5 | 5.1520 | 5.3081 | 5.4684 | 5.6330 | 5.8019 | 5.9753 | 6.3359 |
Ordinary Annuity
Ordinary annuity refers to equal payments paid by the annuitant at the last of the specified period for a fixed time. Moreover, the payments of an ordinary annuity can occur as frequently as every week, while in practice they are generally made annually, semi-annually, quarterly or monthly.
Opposite of the annuity due table is the ordinary annuity. However these two methods are not similar to the financial product known as an annuity, but they are related.
Features :
- Payments at the end of each period
- One example for an ordinary annuity is Consistent quarter stock dividends
- Bonds generally pay interest at the end of every six months
Time Value of money
The present value of the annuity due is a difficult topic to discuss since it relates to the topic of the time value of money. Time value of money explains that if an individual is given $1 today, its worth is more than the same $1 from five years now.
This happens due to inflation and the changing value of money along with its potential to earn interest. Therefore, the present value of annuity due table refers to calculating the value at the end of given periods using the current value of money.
Another way it can explain is how much an annuity due table will be worth when the payments get complete in future, compared to the present. Therefore, This situation becomes vice versa for future value.
Present Value of Annuity Due
The annuity due can be calculated keeping the time value of the money in mind. One way is the present value of the annuity due table. So, It is used to derive the current value of cash payments that are to be made in predetermined amounts on predetermined future dates.
It uses the basic present value concept for annuities, except that cash flows are discounted to time zero. The calculation is made to decide either an individual should take a lump-sum payment or a series of cash payments in the future.
Whereas, The present value is calculated with the discount rate, which is nearly equal to the current rate of return on the investment. Moreover, This must be noted that the higher the discount rate, the lower will be the present value and vice versa.
Annuity due Formula
The annuity due formula to find the present value of annuity due table where the payments are made at the start of each period is:
| PVAD= PMT + PMT([1 – (1+r)^-(n-1)]r) Or PV(annuity due)= C x [(1-(1+i)^-n)i]x (1+i) |
Where PMT = each annuity payment amount
r = interest rate
n = number of periods over which payments are made
PVAD = present value of an annuity due
The factor used to calculate the present value is derived from the present value of the annuity due table that lays out applicable factors by interest rate and the period in a matrix.
Example
Example 1: To calculate the present value of an annuity due table to future rent payments specified in the lease. So, Suppose an individual pays $1000 per month as rent. Therefore, below is an explanation of what it will cost the person for the next five months, in terms of the present value with 5 % interest.
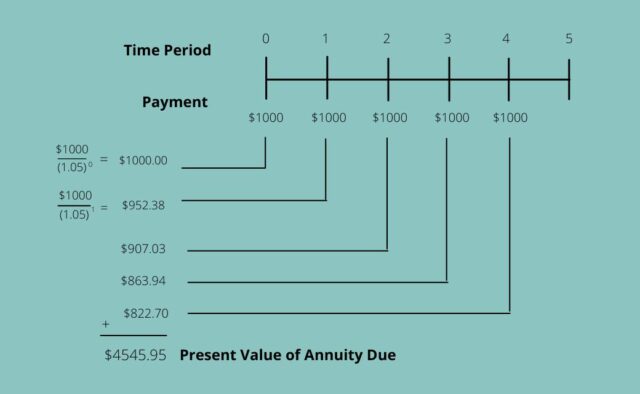
So, PV(annuity due)= 1000x [(1-(1+0.05)^-5)0.05] x (1+0.05)
=$4545.95
Example 2
XYZ International paid a third party $100 at the start of each year for the upcoming three years for rights to a key patent. Therefore, Find the cost to XYZ, if it has to pay the whole amount with an interest rate of 5%.
P= 100 + 100 [(1-(1-0.05)-(3-1))0.05]
= $285.94
Therefore, $285.94 refers to the current value of $100 for three payments with a rate of 5%.
Future Value of Annuity Due
The future value refers to the total of all payments of the future values in the annuity. Therefore, it explains that it is possible to add up all future value of cash flows but not pragmatic if more than a couple of payments are there.
If the future value of all payments is to be found manually, then the explicitly about termination of annuity and inception is important. In the case of an annuity due table since the payments occur at the start of each period, so the first payment is at the inception of the annuity while the last occurs one period before the termination.
Therefore to calculate the future value of annuity due table more easily, we have a formula. For which we need to know the:
- An interest rate of the account the payments are deposited in represented by “r” or “i”
- Payment amount/ cash flow per period depicted by “C”, “pmt” or “p”
- Number of periods per year known by “n”
Annuity due Formula
FV(annuity due)= C x ( [(1+i)^n -1]i ) x (1+i)
Example
This method results in higher values taking into account payments occurring at beginning of each period. Furthermore, The reason why values are higher can be explained that the beginning period payment leads to more time to earn interest.
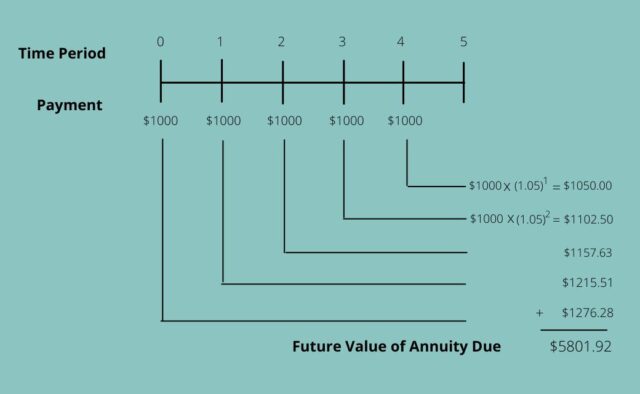
In Example 1 discussed above,
FV(annuity due)= 1000 x ( [(1+0.05)^5 -1]0.05 ) x (1+0.05)
=$5801.92
The above example explains that the amount of interest gathered on the first $1000 receives interest for 5 years making it $1276.28. While the last instalment received, totals an interest of $1050.00 only since it was deposited for one year.
Present Value of Ordinary Annuity
Concerning the future value, the present value explains the amount of money required now to occur in a series of payments in the future, assuming a fixed interest rate.
Also, the same formula of the present value of an annuity due table is used for the present value of an ordinary annuity where payments occur at the last of each period. But, Except that the extreme right side adds an extra payment. This explains when each payment occurs one period sooner than under an ordinary annuity.
Ordinary annuity Formula
The following is the applicable ordinary annuity formula that can be used to directly find out one figure of the present value in the ordinary annuity:
PV(ordinary annuity) = C x [{1-(1+i)^-n} i ]
Example
Using the example of five instalments with $1000 payments made for 5 years with a 5% interest rate. So, calculate the present value of the ordinary annuity.

PV(ordinary annuity) = 1000 x [{ 1- (1+0.05)^-n} / 0.05]
= 1000 x 4.33
=$4329.48
Future Value of Ordinary Annuity
The future value measures how much regular payments will be worth given a specified rate of interest in the future at some point. Likewise, if an individual thinks to invest a specific amount each year or month, future value tells him how much will he accumulate as of a future date. Moreover, If a person is making regular payments on a loan, the future value helps in determining the total cost of the loan.
Formula
Rather than calculating payment for each year individually and adding them, the annuitant can use a formula which directly gives the figure of how much money will there at the end:
FV ( ordinary annuity)= C x [ {(1+i)^n – 1} i ]
Where, C = cash flow per period
I = interest rate
N = number of payments/ time period invested
Example
Considering the above example, the concept of the time value of money tells that any sum has more worth as compared to the future like the first $1000 payment is more than the second and so on. Therefore, as the example states $1000 has been invested every year with 5% interest for the next five years.
Therefore, below explains how much an investor has at the end of five years keeping inflation (price level accounting) in find.

FV (ordinary annuity) = $1000 x [ {(1+0.05)^5 – 1} 0.05]
= 1000 x 5.53
= $5525.63
Annuity Due vs Ordinary Annuity
Following descibes the major difference between the two kinds of annuities in brief to get a clear understanding of the concepts and relation between them:

Payments
The major difference to explain the concept of an annuity due vs ordinary annuity counts the period at which the payments occur. The payments for the ordinary annuity are made at the end while the opposite persists for an annuity due table where payments are made at the start of the interval.
Annuity due vs Ordinary Annuity also differentiates from example. The annuity due table includes rent and smartphone bills while ordinary annuity quotes mortgage, loan, dividend and bond interest.
Present value
Another difference for an annuity due vs ordinary annuity is that the present value of an annuity due table has a greater figure than an ordinary annuity. This happens due to the principle of the time value of money since annuity due table payments are received earlier.
However, the benefit from ordinary annuity gains by holding the money for longer (for the interval). Conversely, annuity due benefits if the annuitant wants to receive the money sooner. Also, In the annuity due table, each period discounts one period less concerning a similar ordinary annuity.
Relationship in Equation Terms
PV of annuity due = PV of ordinary annuity x (1+i )
This explains that when the present value of ordinary annuity multiples with (1+i ), it shifts the cash flow to one period back towards time zero.
Future value
Similar to discussed for present value, the future value of annuity due table is higher than ordinary annuity by the similar factor of ( 1+i ) periodic interest rate. Also, Each cash flow or transaction compounds for an additional one period to an ordinary annuity.
Conclusion
Therefore, the annuity due table explains a quick reference for both present and future value, making the annuitant plan for investments. Since present value considers payment concerning present worth and future value the gain at the end of the period, we have a different annuity due table. Moreover, there is another kind of annuity referring to an ordinary annuity which is the opposite of annuity due.