Law of returns to scale is one of the most important metrics to consider while running a factory. In order to understand how the change in input makes changes to the output.
The Law of returns to scale discusses the change and rate of change in output due to the rate of change in the input.
In other words, the law of returns to scale illustrates the proportionate or percentage change in the amount of input changes the amount of output. The Law of returns to scale is the concept of production. Whereas, the cardinal utility is the concept of individual demand.
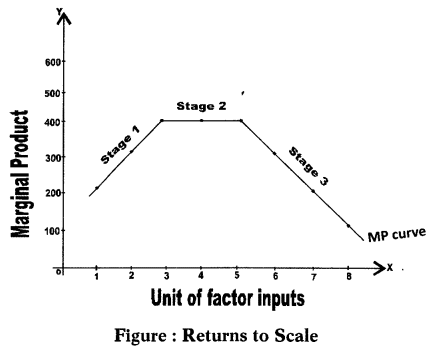
The degree of change in output varies with the change in the number of inputs.
For example, an output may change by a large proportion, the same proportion, or a small proportion with respect to a change in input.
Based on these possibilities, the law of returns to scale can be classified into three categories:
i. Increasing Returns To Scale
ii. Diminishing Returns To Scale
iii. Constant Returns To Scale
Increasing Returns to Scale:
The first law of returns to scale is increasing returns to the scale, which is referred to as when an organization has a greater proportional change in the output than in input.
If an organization has doubled the quantity of input, and the resultant output is more than double, than this is called increasing returns to scale.
Moreover, the average cost of production decreases with the increase in the scale of production. At this stage, an organization enjoys high economies of scale.
For example:
Example of the law of returns to scale in increasing returns to scale, Suppose a pencil manufacturer invests in the inputs like labour and capital so the following results are shown :
| UNITS OF LABOUR | UNITS OF CAPITAL | % CHANGE IN INPUT | OUTPUT | % CHANGE IN OUTPUT | RETURNS TO SCALE |
| 1 | 3 | – | 10 | – | |
| 2 | 6 | 100% | 30 | 200% | INCREASING |
| 3 | 9 | 50% | 60 | 100% | INCREASING |
As the manufacturer goes on, the table clarifies that enlarging his business by investing in respective inputs. As the investment starts to increase with each successive stage the level, of output also starts to increase, which can be shown in column 5.
Therefore, the manufacturer gets more percentage or nearly double in the above example from the invested inputs. It should also be noted that such a case arises when the average cost is low due to economies of scale.
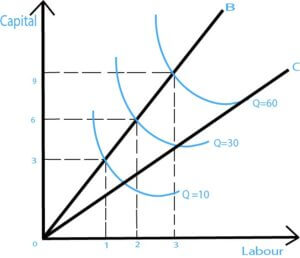
The above graph represents the relation between the cost of production and output. The X-axis and Y-axis represent the change in input. Q denotes the change in the respective output and line B and C showcases the product lines along which the manufacturers expand. Here the cost per product falls with the increase in production.
Diminishing Returns to Scale
The second law of returns to scale is diminishing returns to scale; when the proportionate change in output is less than the proportionate change in input, it is called diminishing returns to scale.
In this case, if the level of input is doubled, so the output which is gained is less than doubled.
| UNITS OF LABOUR | UNITS OF CAPITAL | % CHANGE IN INPUT | OUTPUT | % CHANGE IN OUTPUT | RETURNS OF SCALE |
| 5 | 15 | – | 100 | – | |
| 6 | 18 | 20% | 120 | 10% | DECREASING |
| 7 | 21 | 16.6% | 130 | 8.3% | DECREASING |
If all the input is increased, then the output will be:
- Constant returns to the scale, and the output is double from the previous one.
- Decreasing returns to scale, the output is less than double from the previous one
- Increasing returns to the scale, the output will be more than double the previous output.
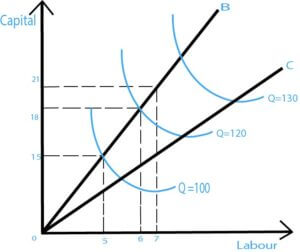
Let’s assume, in input markets firm is a perfect competitor (constant factor cost) and a homothetic production. A firm experiencing constant returns will have constant long-run average costs; in case of decreasing returns will have increasing long-run average costs. And increasing returns will have decreasing long-run average costs.
However, if the firms do not get the correct competitive factor markets it can break the relationship.
For example, if there are increasing returns to scale in some range of output levels, increasing the purchase of an input boom the input per cost as the firm is so prominent in 1-2 markets.
In that level of output, firms could have diseconomies of scale. In some cases, output-level firms could have economies of scale if they get a huge discount on inputs.
Constant Returns to Scale:
The third law of returns to scale is constant returns to scale. In constant to scale, the proportionate change in input is equal to the proportionate change in output.
For instance, the quantity of input is doubled; in this case, output quantity is also doubled. This takes place in the long run (where labour and capital are variable factors).
| UNITS OF LABOUR | UNITS OF CAPITAL | % CHANGE IN INPUT | OUTPUT | % CHANGE IN OUTPUT | RETURNS TO SCALE |
| 3 | 9 | – | 60 | – | |
| 4 | 12 | 33% | 80 | 33% | CONSTANT |
| 5 | 15 | 25% | 100 | 25% | CONSTANT |
Graph Of Constant returns and economies of scale
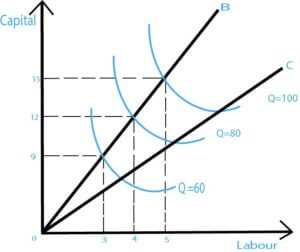
There will be economies of scale to some extent if the firm has constant returns to scale.
In this situation, the firm can face lower average costs with increased output. The reasons for these are:
- Buying a huge quantity of input can result in lower costs.
- Economics in marketing and finance.
Frequently Asked Questions (FAQs)
Explain the law of returns to scale economics
The law of returns to scale economics refers to the feature of many production processes in which the cost of producing per unit falls as the scale of production rises.
What are the 3 laws of returns to scale?
There are three possible types of returns to scale: increasing returns to scale, constant returns to scale, and diminishing (or decreasing) returns to scale.
What is the law of returns to scale?
The law of Return to Scale in Production Functions
Changes in output when all factors change in the same proportion are referred to as the law of return to scale. This law applies only in the long run when no factor is fixed, and all factors are increased in the same proportion to boost production.